ページランクの計算方法原理分かりやすい例です。
ウェブ世界が、次のようにたった3つのウェブページから構成されていると仮定します。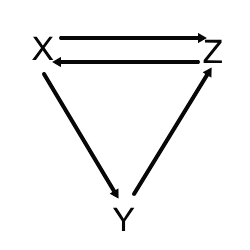
このリンク関係は、次のような簡単な数式で記述しえます。下記の式の左のX・Y・Zのそれぞれのウェブページについて、右側の式で他のページとの関係を示すと考えてください。
①X=Z Xは、Zの発する唯一のリンクを受けています。
②Y=X/2 Yは、Xの発する2つのリンクのうち、ひとつを受けています。
③Z=X/2+Y Zは、Xの発する2つのリンクのうちひとつを受け、かつ、Yの発する唯一のリンクを受けています
行列では、次のようにします。
リンクがされている場合には、1を入れる.
| X | Y | Z | |
| X | 0 | 0 | 1 |
| Y | 1 | 0 | 0 |
| Z | 1 | 1 | 0 |
列の合計を1にする。
| X | Y | Z | |
| X | 0 | 0 | 1 |
| Y | 0.5 | 0 | 0 |
| Z | 0.5 | 1 | 0 |
この行列を適当な初期ベクトル(=任意の数値の組み合わせのことです。この例では、1,0,0とします。)にかけて、反復計算して得られた数値
(設定した計算精度で同じ数値の繰り返しになるまで)が、パラメーター d を考慮しない場合の(即ち1)ページランクの基礎数値です。
なお、正確に言えば、リンク関係をグラフとみなし、隣接行列(リンクがある場合には、上記のように列に1を入れるのではなく行に1を入れ、行の合計を1にすることを意味します。)と考えるのが、
根本発想ですが、このウェブサイトでは、上記形式で統一しています。
ページランクの算出が、上記のような手法で、算出されていることは、ページランクに関する特許に示されている、下記の式から明白です。 p∞=limAnp0 (n→∞)
なお、例えば、p2 =Ap1=A2p0である旨、特許文書に明記されています。
p0が、初期ベクトル(この例では、1,0,0)。Aは、英語でグーグル行列と呼ばれる下記の行列です。
A=(α/N ×1 )+(1-α)B この行列の詳細は、現実のページランク算出方法を見てください。1
は、太字にしていますがベクトルではなく、行列です。
変数の数が、少なければ、計算式の入力にそれほど時間は、かかりませんので、エクセルで簡単に計算できます。べき乗法又はパワー法=power methodと呼ばれる良く知られているごく簡単な計算方法です。
上の行列の例では、エクセルでは下記のように43回目の反復で、収束します。
(注)
エクセルの場合、計算は、10-16 程度で、打ち切りとなります。このため、計算精度は、10-16とお考え下さい
| 1回目 | 2回目 | 3回目 | 4回目 | 略 | 41回目 | 42回目 | 43回目 | |
| X | 1 | 0 | 0.5 | 0.5 | 0.400001 | 0.4 | 0.4 | |
| Y | 0 | 0.5 | 0 | 0.25 | 0.2 | 0.2 | 0.2 | |
| Z | 0 | 0.5 | 0.5 | 0.25 | 0.4 | 0.4 | 0.4 |
ウェブ上で、ページランクの数値計算原理を紹介されているウェブページがありますが、むしろ誤解を招くだけであると考えます。
Google の秘密 - PageRank 徹底解説の数値計算例で検証しました。
詳細は、ページランクへの誤解ご参照。
8サイト間の例です。ページランクの数値が、確率を示すものであることが、理解いただけるでしょう。
次のようなリンク関係を想定します。(リンク関係図と表は、http://www.ams.org/featurecolumn/archive/pagerank.htmlから借用しています。)
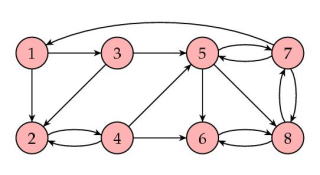
スタート:①からスタートします。
1回目:ウェブサイト①は、②及び③にリンクしています。各0.5を配分
2回目:①のリンク先②は、④のみへリンクしています(0.5を配分)。また、①のリンク先③は、②と⑤へリンクしています(各0.25配分)。
3回目:②は、④のみへリンクしています(0.25配分)、④は、②⑤⑥へリンクしています。
(⑥は、0.25で②⑤は、0.1666をそれぞれ配分)
⑤は、⑥⑦⑧へリンクしています。(⑥のみ0.25、⑦⑧は、0.0833333を配分)
以降は、順次、数値計算します。61回目で終わりました。なお、最終的に得られた数値をstationary distribution vectorと呼び、訳せば、定常分布ベクトルです。(=steady-state vector) 上記のようなパワー法による数値計算で、主固有ベクトル(=ページランク)へ収束することは、既に知られています。Handbook of linear algebra(編集者:Kenneth H. Rosen) Adobe Reader 版682頁より)
| ウェブサイト | スタート | 1回目 | 2回目 | 3回目 | 61回目 | |
| ① | 1 | 0 | 0 | 0 | 0.06 | |
| ② | 0 | 0.5 | 0.25 | 0.1666 | 0.0675 | |
| ③ | 0 | 0.5 | 0 | 0 | 0.03 | |
| ④ | 0 | 0 | 0.5 | 0.25 | 0.0675 | |
| ⑤ | 0 | 0 | 0.25 | 0.1666 | 0.0975 | |
| ⑥ | 0 | 0 | 0 | 0.25 | 0.2025 | |
| ⑦ | 0 | 0 | 0 | 0.0833 | 0.18 | |
| ⑧ | 0 | 0 | 0 | 0.0833 | 0.295 |
これが、ページランクの計算方法の原理です。実際の数値計算では、パラメーター d(ダンピングファクター) が加わります。
何故なら、ダンピングファクター(d<1)がないと、事実上、数値計算(パワー法)ができません。
論文の中で、ページランクの考案者は、「Note that the PageRanks form a probability distribution over web pages, so the sum of all web pages' PageRanks will be one<.」と明言し、計算対象の全てのウェブページのページランクの合計は、1になるとしていますが、これは、上記のような手法で算出されているからです。
①最後の数値(=ページランク)は、例えば、ある人が、サイト①(例えば、Google)からスタート(=検索)し、リンクをたどる場合に、最終的にどのサイトで終わるのかの可能性(確率)を意味することが、理解いただけるのではないでしょうか。(ランダムサーファーモデル参照)
②仮にサイト8に、10のウェブページがあった場合、上記の例では、0.295の数値が、ウェブサイト内の各ページへ再配分される形式で、各ウェブページのページランクが、決定されていると推測されます。計算式は、全く不明。(Google行列の数値計算対象は、あくまでも、外部とリンク関係にあるウェブページのみです。)
(注)内部リンクの扱いについては、特許文書にて、A modification to avoid drawing unwarranted attention to pages with artificially inflated relevance is to ignore local links between documents and only consider links between separate domains. と明記され、数値計算上無視されます。
意訳:意図的に増加させた内部リンク(=関連)によって、ウェブページへ不当な関心を引き寄せることを防ぐ修正(方法)は、ウェブサイト内の内部リンクを無視し、別々のドメイン間のリンクのみを(ページランク計算対象として)考慮することである。
③上記の例では、理解しやすいように、1と0のみからなるベクトルから計算を初めていますが、初期ベクトルは、任意に選べますので、実際には、特許文書によれば、全てを1/Nにして、計算しているようです。
(注)
グーグルページランクの生の算出数値(浮動小数点数)は、当然、近似値にすぎません。容易に近似値を求めうるパワー法の長所ですが、同時に有効な近似値は、どのレベルかという問題が生じます。規模が、大きくなれば、ある方が主張するように「いつまでたっても計算が終わらない」というのは、当然であり、問題の核心は、どのレベルが有効な(意義を有する)近似値であるのかという点なのです。
論文PDF版の図5をみると、10-8レベル程度になった時点で、反復計算を打ち切っています。なお、論文の図5の縦軸は、指数目盛です。(特許では、100回程度の反復を行うとしています。)
一方、反復回数については、ダンピングファクター d の値が、大きく影響します。
①例えば、d=0.99の場合、意味のある近似値(10-8レベル)を得るには、約1800回の反復を要するに対し、d=0.85の場合、114回の反復で、有意義な近似値(10-8レベル)を得ることができるそうです。Deeper inside pagerank 6.1Changing α より。理論面から検討しています。
②一方、この論文(PDF版、執筆者は、同じスタンフォード大学の別人)では、実用的には、10回でも有効であると結論付けています。また、ページランク考案者も、特許文書その他で、反復をあまり多く行う必要はないと再三強調するとともに、計算対象行列の規模は、近似値を得るための反復回数には、全く影響がない旨を指摘し、グラフを掲げています。
以上をまとめると、google創設者両名が、d=0.85 (α=0.15)と設定したことは、有効近似値算出のためには、極めて有効な手法であったというのが、英米の学者の評価のようです。
つまり、計算対象の規模に比べ「収束は早い」と一般には考えられています。(0.85という設定値は、理論上、10-16程度まで計算すれば収束に時間がかかるはずが、意義のある近似値を10-8レベルと仮定すれば、収束は早いという趣旨です。)
なお、α=0.15(d=0.85)とするリンク関係の修正がなければ、理論上、単一のページランクベクトルを算出しえません。
広 告

オリジナルボールペンを小ロット(10本~)から作成します。
スマホで撮影した写真でもOKで、メール送付で簡単作成。
結婚記念・ペットなどあなたの大切な思い出を写真に、そして、写真から世界に一つだけのオリジナルボールペン
オリジナルのシャープペンも製作します。ボールペンとシャープペンのセットでのご注文もお安い値段で可能です。
卒団記念 として毎年多数のご注文を承っております
(例年、2月~3月は、卒団記念のご注文が混み合いますので、早期のご注文にご協力をお願い申し上げます)
写真のトリミング(写真の一部を切り抜き)や色彩の調整も無料で行いますので、非常にお手軽にお安く作成できます
次のアイテムがございますので、販促品・ノベルティ・ご当地グッズ・個人様記念品等の用途に合わせてお選びください
(セット品は、ボールペン1本+シャープペン1本で1セットです)
スタンダードタイプ販促品~卒団記念まで幅広い用途
高級タイプ記念品として最適。のし箱入れします
3色ボールペンオリジナルのイラストにピッタリ
素材販売同人グッズとして
スタンダードタイプのセット卒園記念・卒業記念として
高級タイプのセット結婚式の引き出物等に
ユニフォーム型ストラップ付卒団記念のベストアイテム
10,000本以上大ロット画像が立体的に見えノベルティとして最適
送料無料で、消費税込みです。
同人グッズ向けに素材販売も行っています。
オプションでマスコット アクリルチャーム等の取付致します
梱包や台紙につきましても下記のとおり承ります
①OPP袋入れ
②ヘッター吊り下げ式袋
③白箱入れ
④のし箱入れ
⑤台紙の封入
⑥証紙貼り
⑦OPP裏面シール貼り付け
(②~⑦は、オプションです)
お問合せは、
Eメール
お問合せフォーム
電話
0120-519-710
「ゴー(5)イク(19)ナイレ(710)」です
FAX
047-438-1891